る。論証問題に必要な三角形の相似条件を,既習事項の三角形の合同条件から導かせる。さらに, 三角形と比の定理,中点連結定理,任意等分の作図を考えることで,角の二等分線と辺と比の関 係を,仮説に従って証明している。 (2) 生徒についてLesson 31 三角形の相似条件と証明 第5章 図形と相似 <前:L30 三角形の相似条件 の問題 L31 三角形の相似条件と証明 の解答:次> 練習問題1 以下の1~3に示した各組の三角形が相似であることを証明しなさい。 (※辺の長さの単位はcm)3/3時 ・ 三角形の相似条件を用いて証明することができる。 本時の学習内容「相似条件を使った証明を考えよう」を知る。 教科書101ページの例題2を考える。 条件を満たす図をかき、2つの三角形で、辺や角がどのように対応するか考える。 教科書101

数学 中3 46 相似の証明チャレンジ Lv 1 Youtube
三角形の相似条件 証明
三角形の相似条件 証明- Step2 相似な三角形をさがす つぎは、 相似な三角形 をさがそう。 三角形の相似条件にあてはまる2つの三角形をさがせばいいのさ。 念のため、三角形の相似条件を確認しておくと、 3組の辺の比がすべて等しい;・ 角形を見つけ、証明の仕方を知る。 三角形の相似条件を適 の相似条件を確認してから、証明問題に取り組む 言葉や式を使って表して 6 切に使って、説明を書 ようにする。 いる。 相似な三角形を見つけて、その根 くことができる。




証明 合同 相似 が苦手な人へ 教遊者
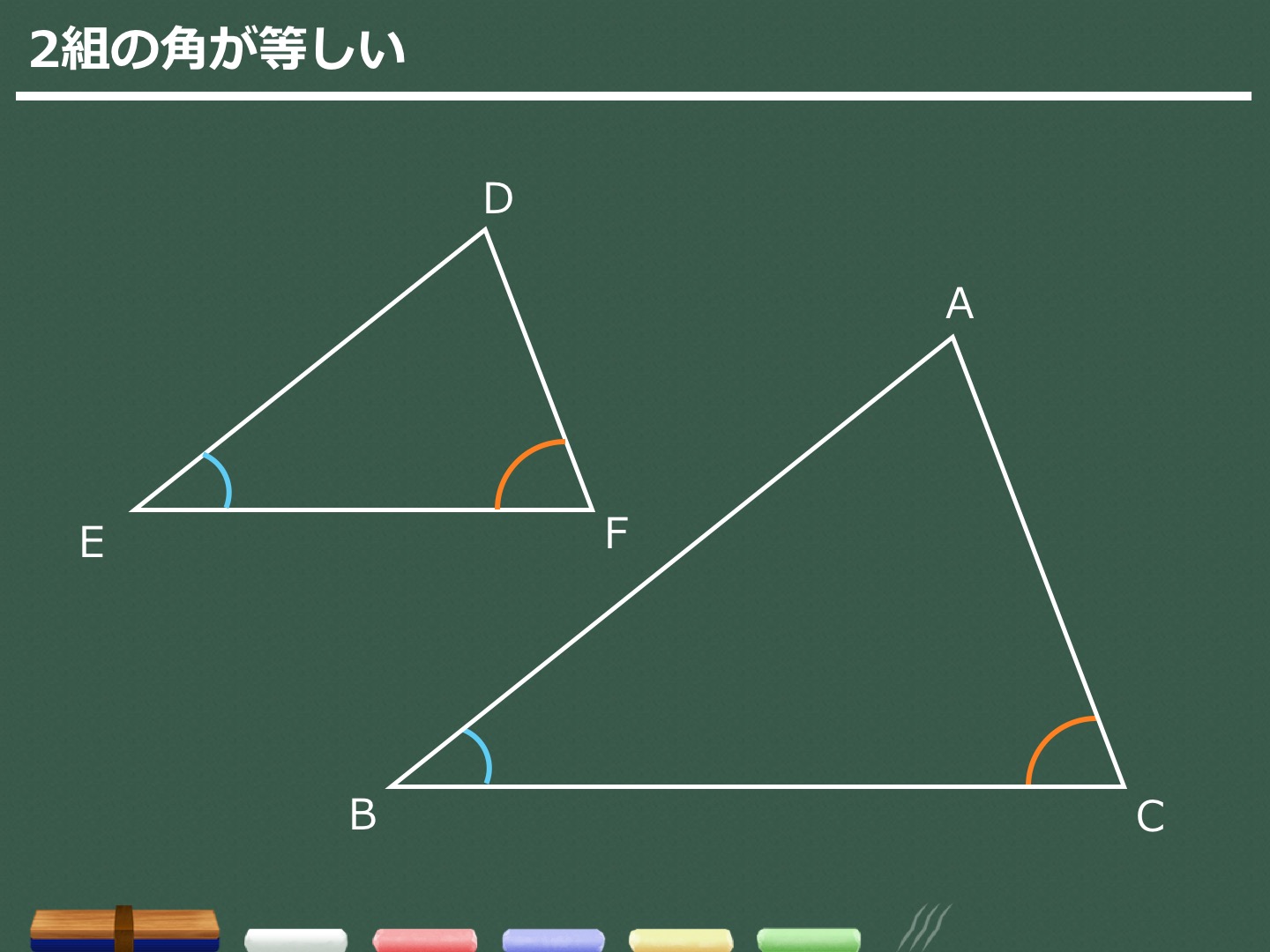
三角形の相似条件 中3数学 証明問題で最も出題されるのがこの相似の証明です。 使う相似条件は99%「2組の角がそれぞれ等しい」と言って過言ではありません。 とにかく等しい角を2つ見つけることを心がけてください。数学・算数 三角形の合同・相似条件についての質問です。 三角形の合同条件と相似条件についてです。 合同条件で二つの三角形が合同になることを中学生に分かるように教えたいのですが、うまい証明法があれ 質問No 三角形の"合同条件・相似条件"の意味について 三角比や正弦定理・余弦定理の理解も深くなる みなさんは、 "なぜ、合同条件を満たせば合同といえるのか、相似条件を満たせば相似といえるのか? "を考えたことがありますか? ここで紹介する合同
や三角形の相似条件を用いて証明する。(7) 理したことの間のつながりを考える。 ・証明としての形式的な表現等にとらわ 第三次 相似な図形の相似比と面積比及び体積比と れず,日常言語に近い形で確認するよ それらの関係について考える。(2) うにする。三角形の合同条件 証明のしくみ 合同条件を使った証明 相似な図形 三角形の相似条件 平行線と線分の比 中点連結定理 相似な図形の面積 相似な立体 相似の利用 中学校1 年 7章 三平方の定理OEは2つの三角形に共通な辺 よって3組の辺が等しいので 合同な図形の対応する角は 等しいので 2等分線になる なぜ、この作図が角の二等分線になるのだろう? D C B o A E
相似な図形/三角形の相似条件/相似の証明:2 辺の比とその間の角/2 組の角が等しい/ 直角三角形など /三角形の相似と長さ/FdData 中間期末製品版のご案内 FdData 中間期末ホームページ 掲載のpdf ファイル(サンプル)一覧 >三角形の相似条件、合同条件を証明して下さい。 「~条件」を証明するってことですよね。 条件を証明することはできるのですかね? そうではなくて、 例えば、合同条件の1つである「2組の辺とその間の角がそれぞれ等し」ければ合同である。三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題 三角形の相似条件と有名な例題3問 具体例で学ぶ数学 本時のねらい 図形の中から相似な三角形を見出し 相似条件を用いて証明することができる Ppt Download



三角形の相似条件 修正 Youtube



相似の証明 2つの正三角形と共通な角 勉強ナビゲーター
2 三角形の相似条件 2つの三角形△ABC,△DEF について, ∠D =∠A,∠E =∠B,∠F =∠C と = = が成り立つならば, この2つの三角形は相似であるといえる。三角形の相似条件を用いて図形の性質を証明す る。 8 三角形の相似条件を用いて図形の性質を証明す る。 2 平 行 線 と 線 分 の 比 1 9 紙の横幅を 3等分する線をひく方法を知り,なぜ その方法で 3等分できるのかを考える。 10 三角形の1辺に平行な直線で他の2辺を切り取るとき の線分の比 (1)三辺の比が等しい場合は比の値を掛ければ互いに合同な三角形になるので相似は明らか(相似の定義?)ですが、 (2)2辺の比とその夾角が等しい場合と (3)2角が等しい場合は どのように証明(説明)すればよいでしょうか?




高校数学a 方べきの定理3パターンの証明と三角形の相似 受験の月
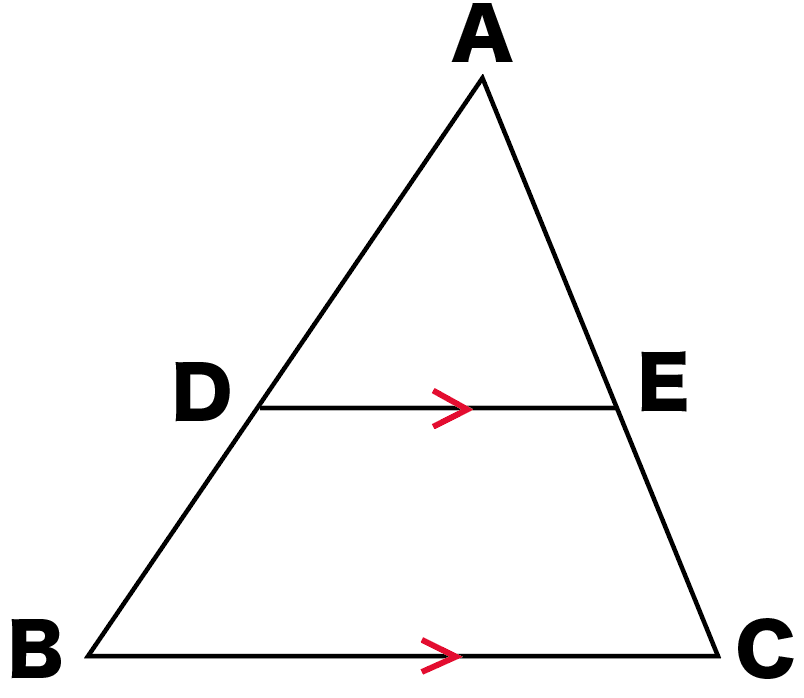



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru三角形の相似条件 3組の辺の比 がそれぞれ等しい 2組の辺の比 と その間の角 がそれぞれ等しい 2組の角 がそれぞれ等しい 合同条件と似ているのがわかるかと思います。 1番目と2番目は「辺」が「辺の比」になり、3番目は「辺の長さに関する条件」がなくなったものです。 ではこの三角形の相似条件をどのように使うのか、実際に問題を解きながら見ていき「二等辺三角形の作図から証明を使って性質を導くことができる。 「定義や定理の用語の意味を理解する。 下の図で、点Aを中心にして直線ℓと交わる円をかき、その交点をB,Cとして、 ABCをかきま
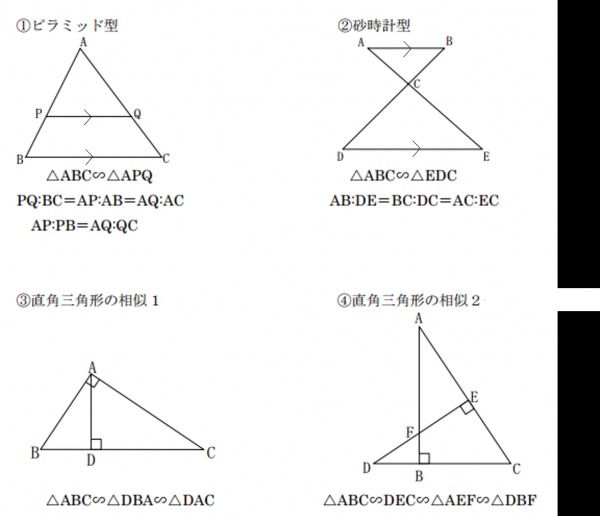



三角形の相似 合同条件 優技録
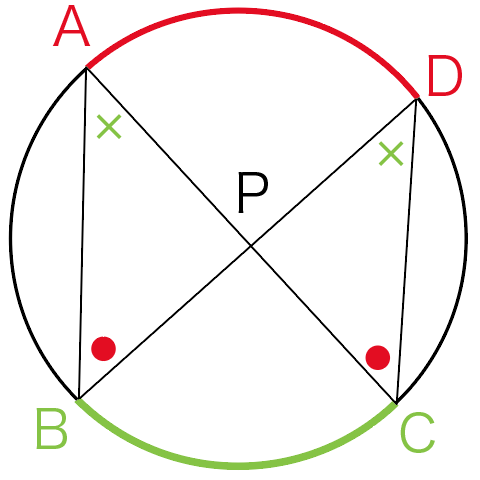



円周角の定理をつかった証明問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく
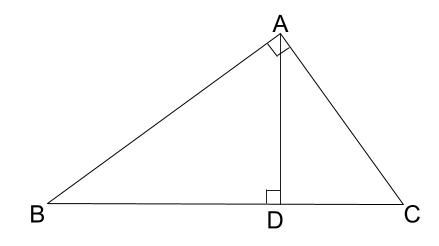
a= b(証明終了) 相似の証明のコツを紹介 中3の数学で習う「相似」についてみていきましょう。 「相似」というのは、2つの三角形が拡大・縮小の関係にあることで、相似条件を満たしていればこの関係にあると証明することができます。三角形 相似条件 証明 三角形の相似条件とは、2つの三角形が相似であることを示すための条件です。 以下の3つの相似条件のうち、どれかが成り立つ場合、その三角形は相似であるといえます。 3組の辺の比がすべて等しい。三角形の相似の証明 (木) 三角形の相似条件には,「対応する3組の辺の比がすべて等しい」「対応する2組の辺の比が等しく,その挟む角が等しい」「対応する2組の角がそれぞれ等しい」の3つがあるが,定期テストや高校入試で出される問題では



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題
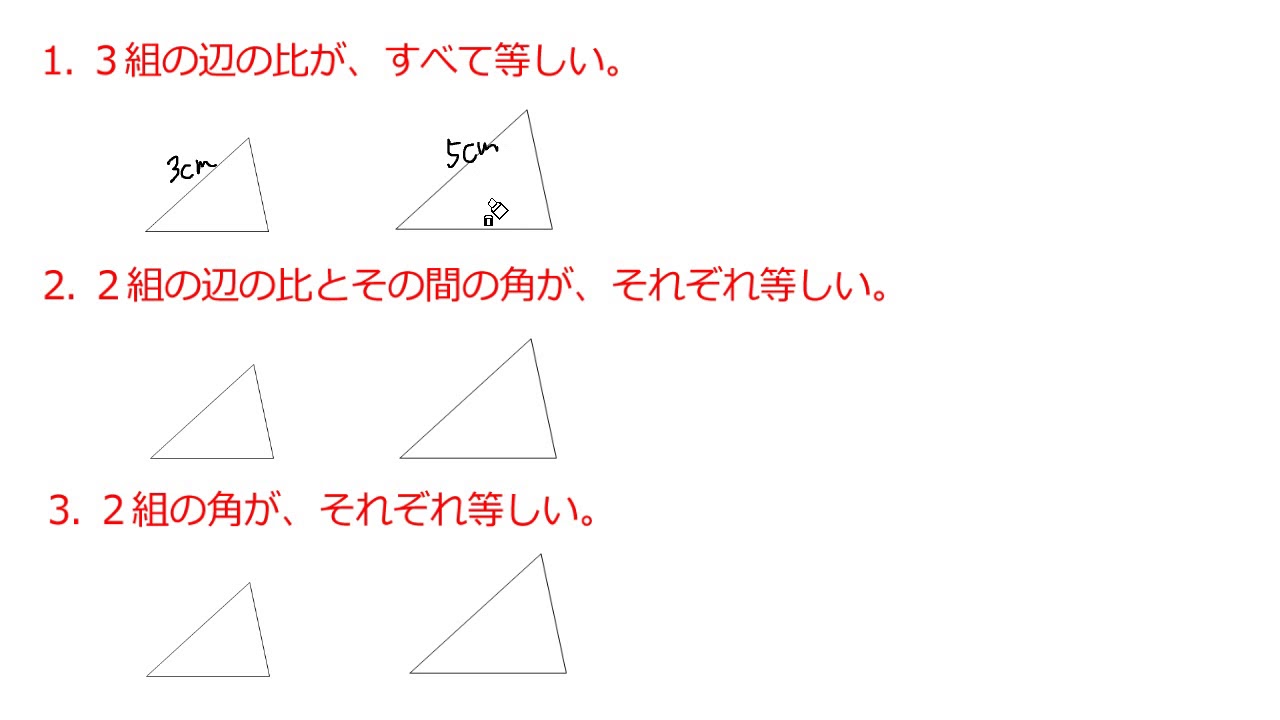
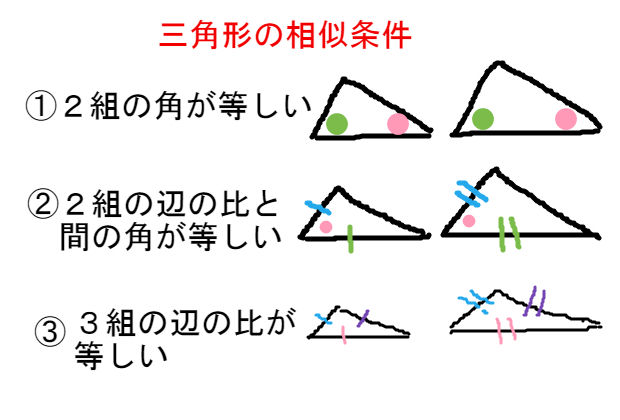
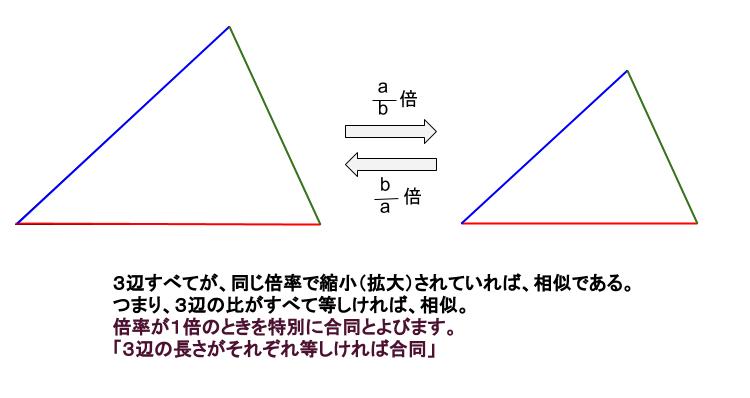
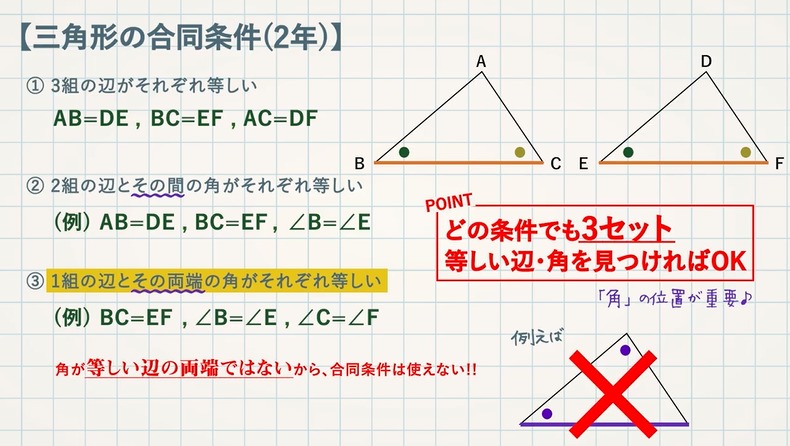
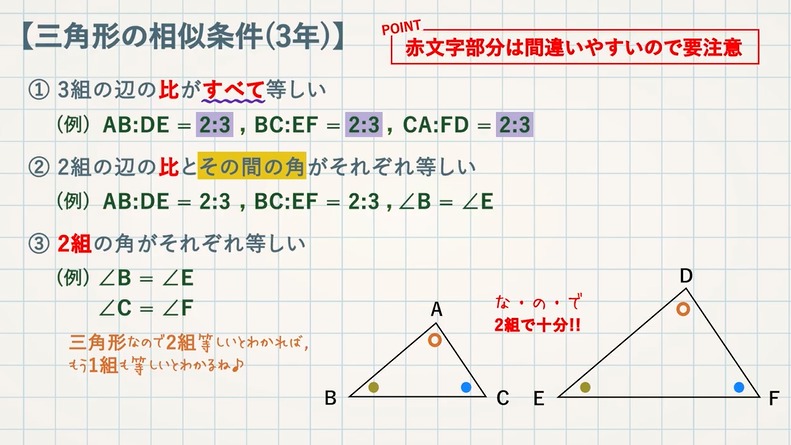
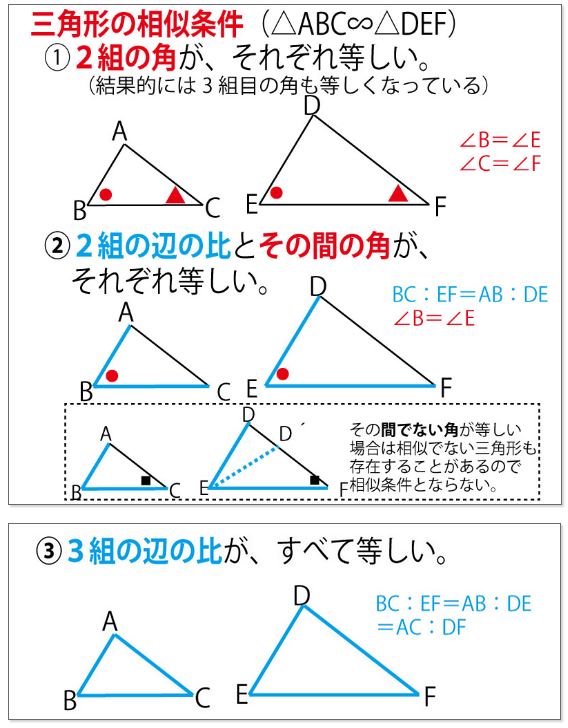
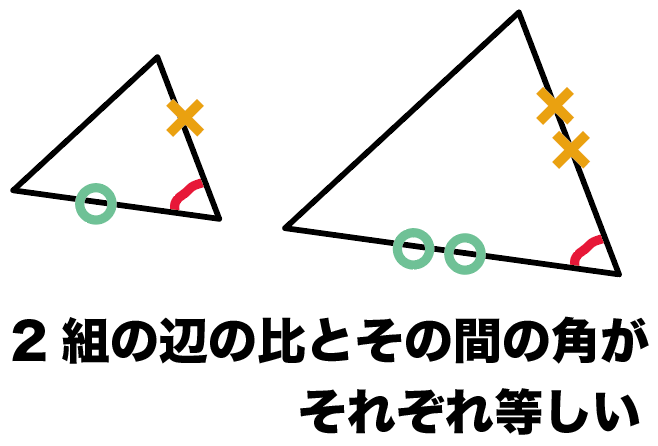
三角形の相似を証明するためには、「相似条件」というものを使います。 相似条件には、以下の 3 つがあります。 相似条件①3 組の辺の比がそれぞれ等しい 3 辺の比がそれぞれ等しければ、相似と言えます。 両方とも 数学の証明 のために必要なアイテムだから、テスト前には覚えなきゃいけないね。 念のためおさらいしておくと、 三角形の合同条件 3つの辺の長さがそれぞれ等しい 2組の辺の長さとその間の角が等しい 両端の角とその間の辺の長さがそれぞれ等しい 三角形の相似条件 3組の辺の比がすべて等しい 2組の辺の比とその間の角がそれぞれ等しい三角形の相似条件( $3$ 年) ① $\textcolor{blue}{3}$ 組の辺の比がすべて等しい (例) $\textcolor{blue}{\rm ABDE=23}$ , $\textcolor{blue}{\rm BCEF=23}$ ,




中3数学 相似 直角三角形と相似 Youtube




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張
三角形の相似条件 三角形の相似条件 とは、2つの三角形が相似であることを示すための条件です。 以下の3つの相似条件のうち、どれかが成り立つ場合、その三角形は相似であるといえます。 3組の辺の比がすべて等しい。 2組の辺の比が等しく、その間の角が等しい。 2組の角がそれぞれ等しい。 このページの続きでは、三角形の図を見ながら、これらの相似条件 三角形の合同条件は定理ですか??公理ですか? 定理を証明するためには三平方を用いる必要がありますし、(証明はカット)三平方を証明するためには相似(合同の親戚だから)以外の方法で示さなくてはなりませんよね?? 助言お願いします。という意味になるように変えることで,三角形の合同条件を三角形の相似条件に変えることができます。 つまり,三角形の相似条件は, 1辺 とその両端の角がそれぞれ等しい→2組の角がそれぞれ等しい となります。 3の条件は,「1組の辺の比とその両端



三角形の相似 合同条件 中学数学 理科 寺子屋塾の復習サイト



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス
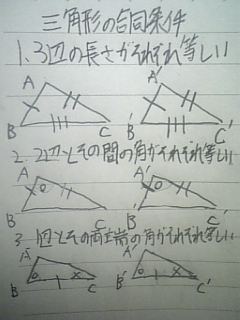



受験数学かずスクール 三角形の合同条件と直角三角形の合同条件と三角形の相似条件



3



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス
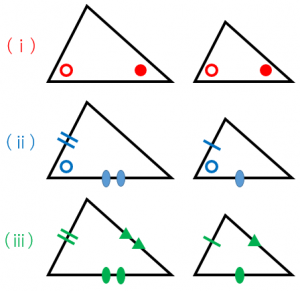



三角形の相似条件と有名な例題3問 具体例で学ぶ数学
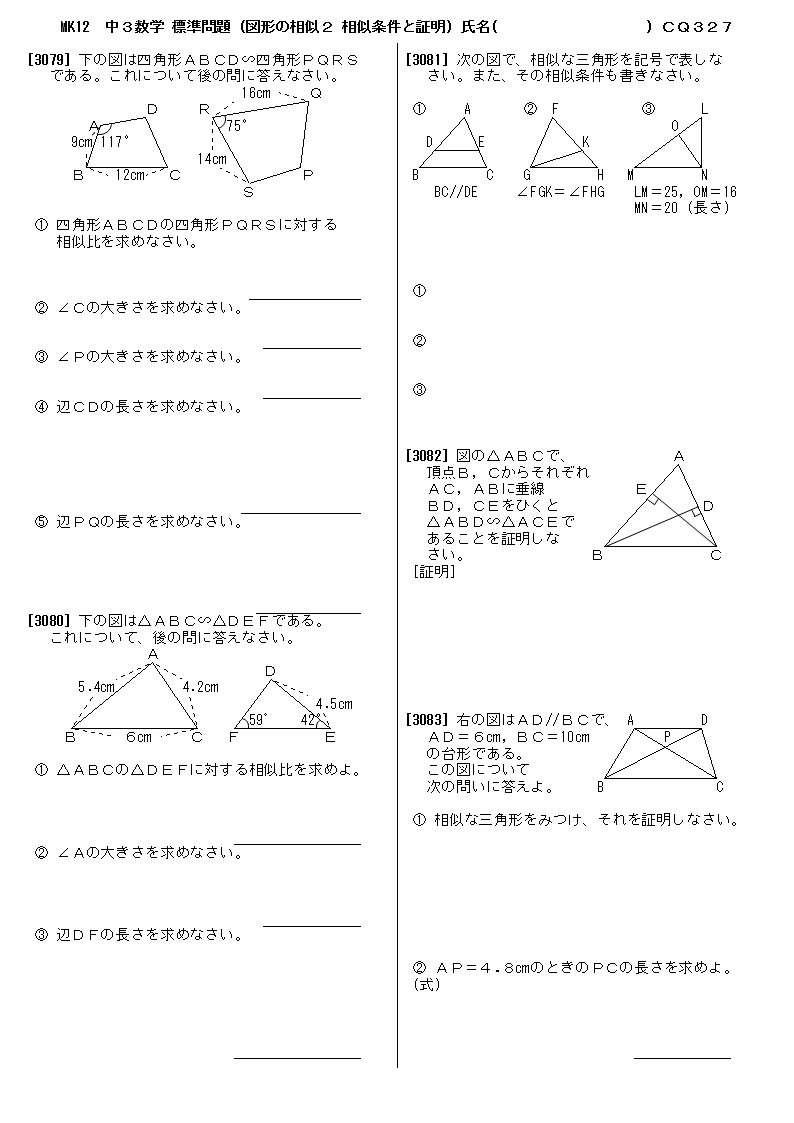



無料 中3数学 標準問題 問題プリント 327 図形の相似2 相似条件と証明



中学数学 三角形の相似条件 中学数学の無料オンライン学習サイトchu Su



中学数学 相似の証明 その2 中学数学の無料オンライン学習サイトchu Su




数学 中3 46 相似の証明チャレンジ Lv 1 Youtube
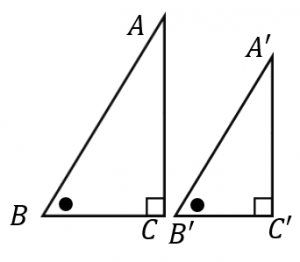



直角三角形の相似条件 具体例で学ぶ数学



Studydoctor三角形の相似条件 中3数学 Studydoctor
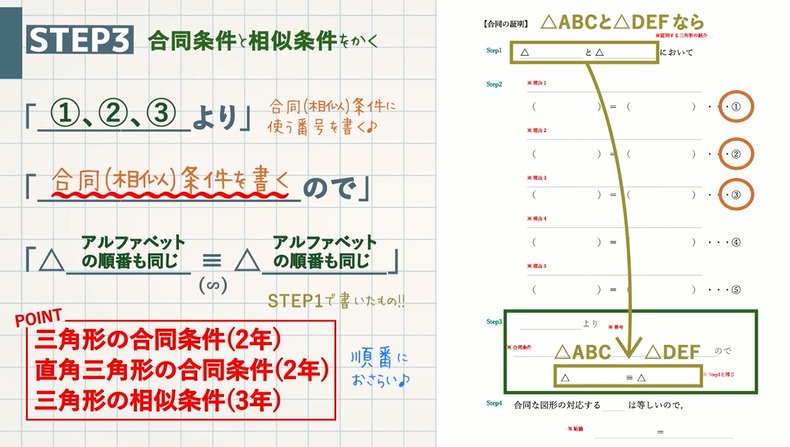



証明 合同 相似 が苦手な人へ 教遊者



1
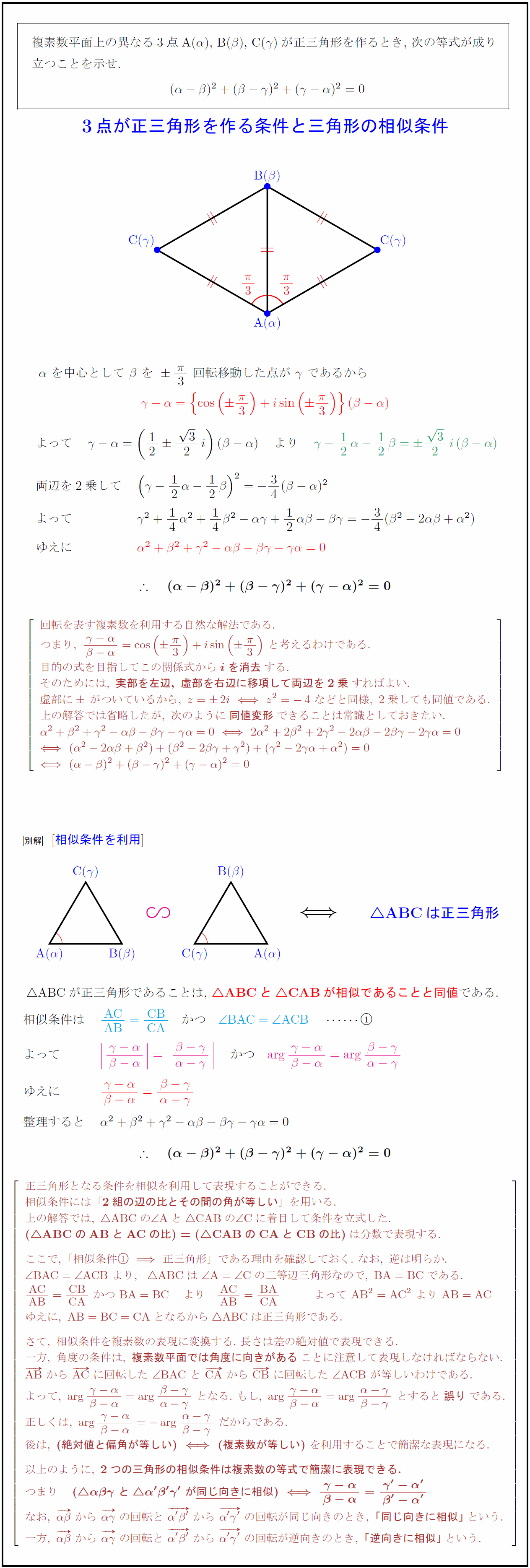



高校数学 複素数平面上で3点が正三角形を作る条件と三角形の相似条件 受験の月




相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学
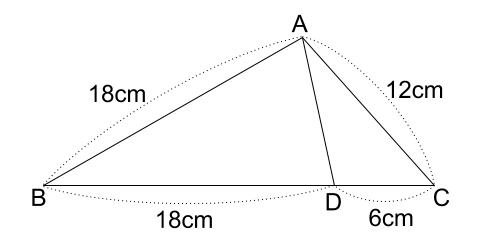



中学数学 相似の証明 その1 中学数学の無料オンライン学習サイトchu Su



相似条件と証明 中学3年 数学クラブ




三角形の相似条件




5章1節2 三角形の相似条件2 数学のすすめ
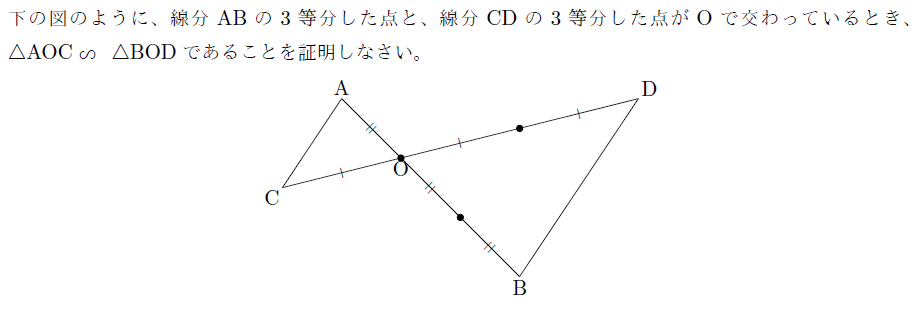



三角形の相似の証明 まなびの学園



三角形の相似の証明 平行線の錯角 勉強ナビゲーター
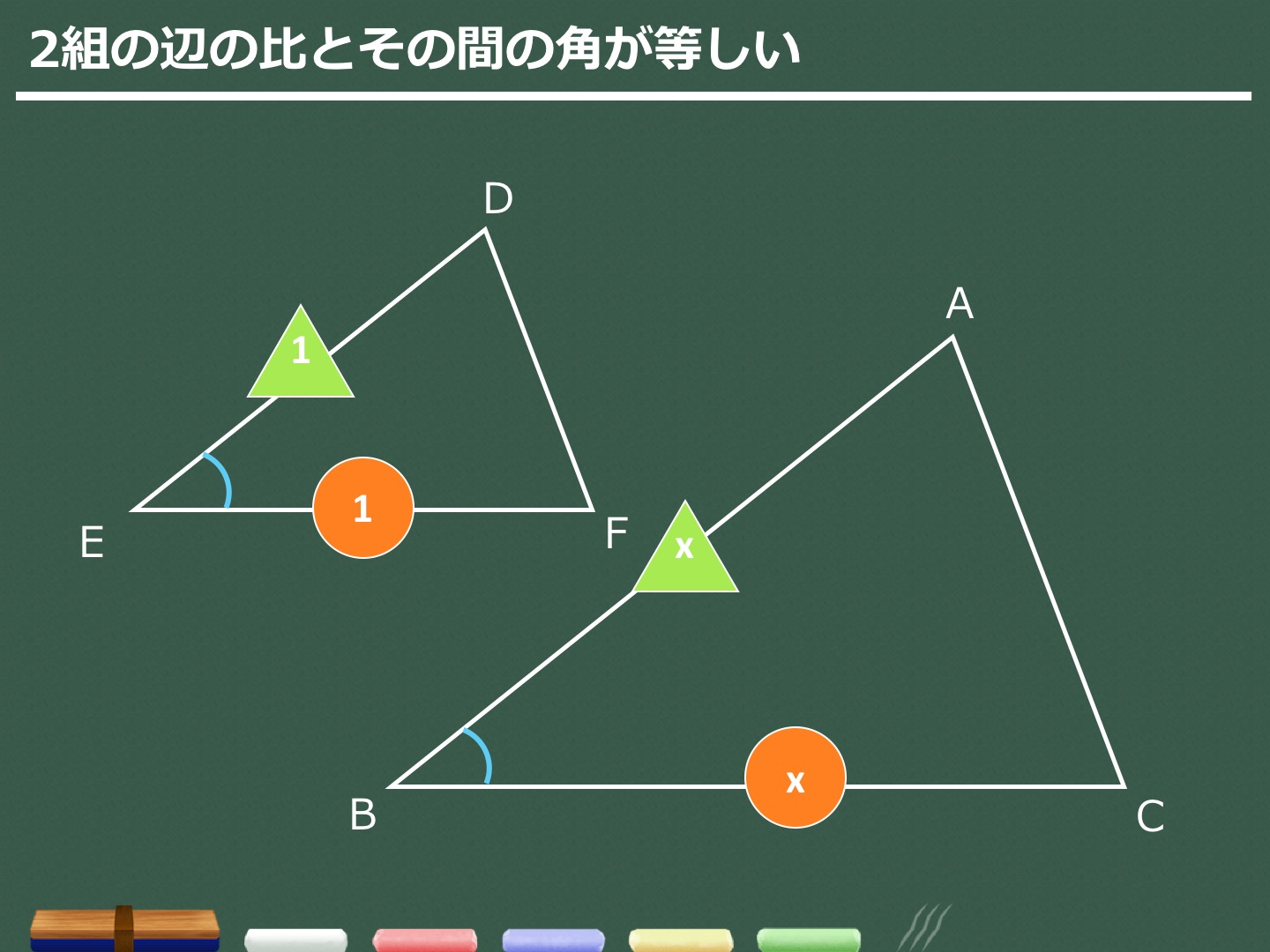



3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ
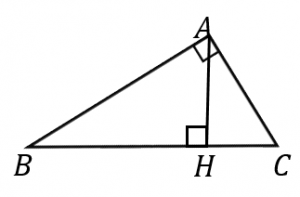



直角三角形の相似条件 具体例で学ぶ数学



証明 合同 相似 が苦手な人へ 教遊者




中学数学 学研教育出版 牧野正博著 三角形の相似条件を利用した証明 2 P 418 113 Mathtriangleの雑記帳
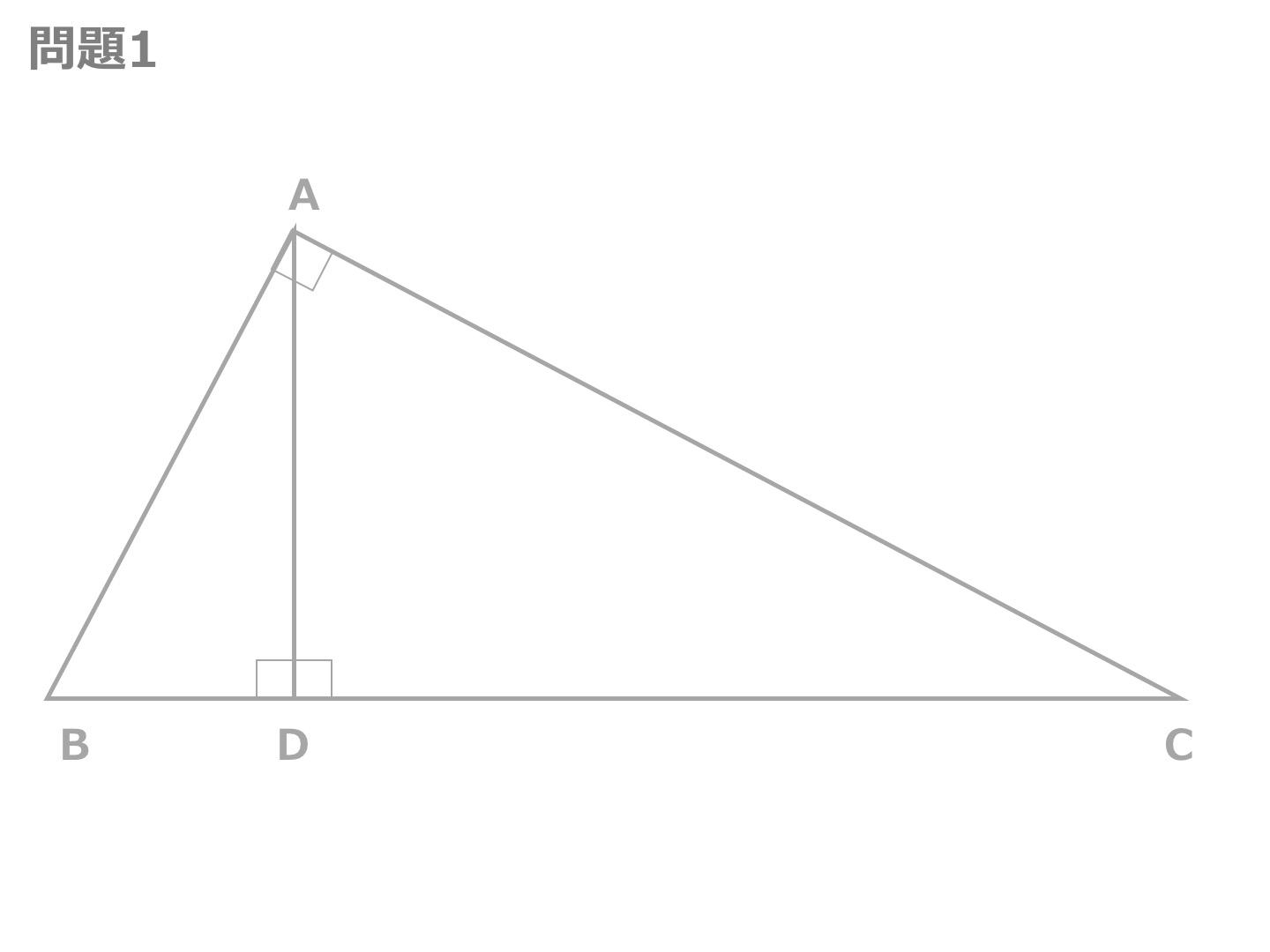



3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ
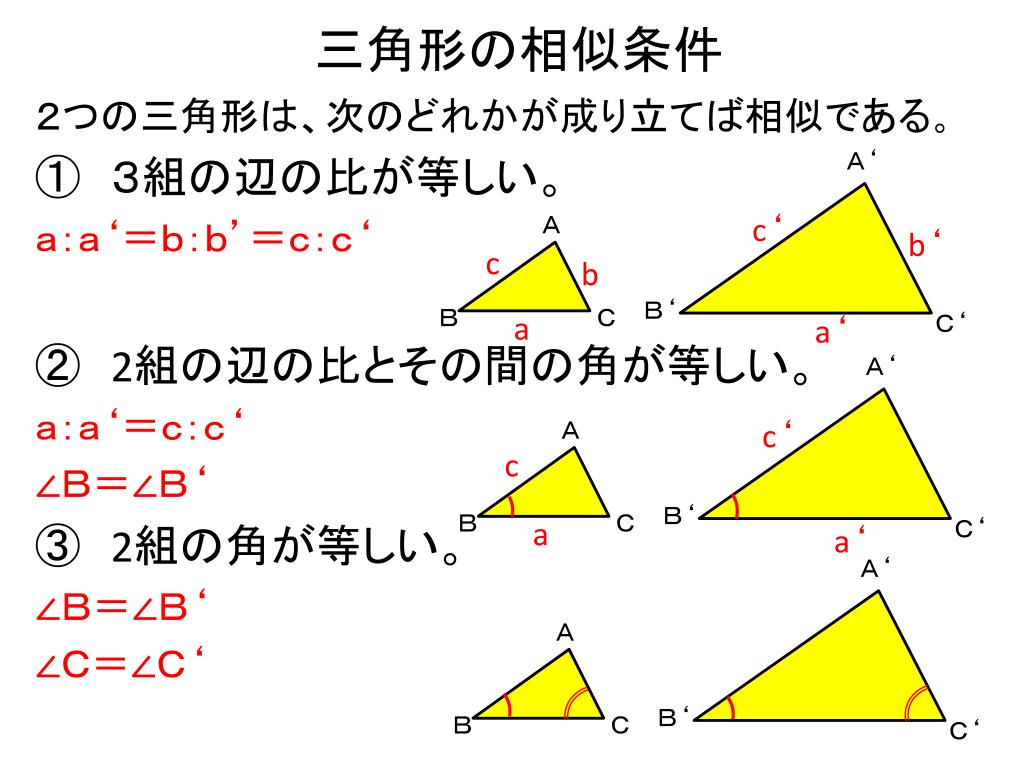



Ppt 相似条件と証明 Powerpoint Presentation Free Download Id




三角形の合同条件と証明問題の解き方 数学fun



証明 合同 相似 が苦手な人へ 教遊者




中3数学 相似な図形 三角形の相似条件を使った証明 2組の辺の比とその間の角がそれぞれ等しい 三角形の中にある三角形との相似の証明 Youtube




この3問がどうしても わかりません 回答お願いいたします もしよければ途中経過も Clear




中3数学 円と相似 の証明問題の解き方のコツ 映像授業のtry It トライイット
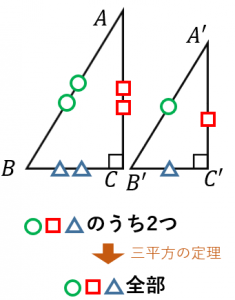



直角三角形の相似条件 具体例で学ぶ数学



1




中学数学 相似の証明問題の書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
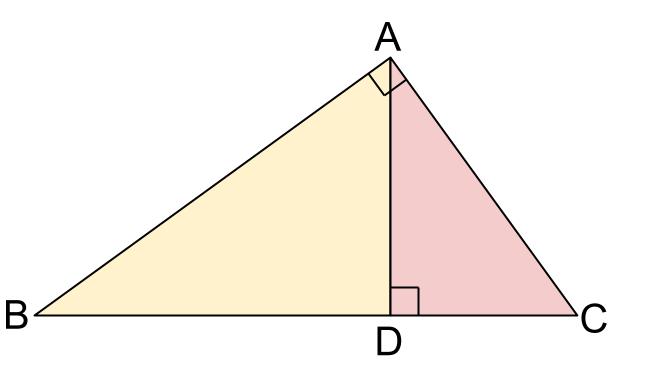



中学数学 直角三角形の相似 中学数学の無料オンライン学習サイトchu Su
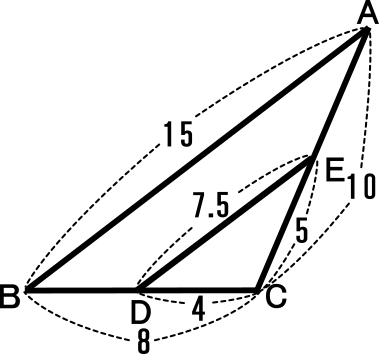



中学3年数学練習問題 三角形の相似条件と証明の問題



中3数学12 図形の相似2 相似条件と証明 基本解説プリント 問題 327




証明 合同 相似 が苦手な人へ 教遊者



三角形の相似条件はゆとり前の言い方はありますか ゆとり教育 Yahoo 知恵袋




三角形の相似条件と基本的な証明 無料で使える中学学習プリント
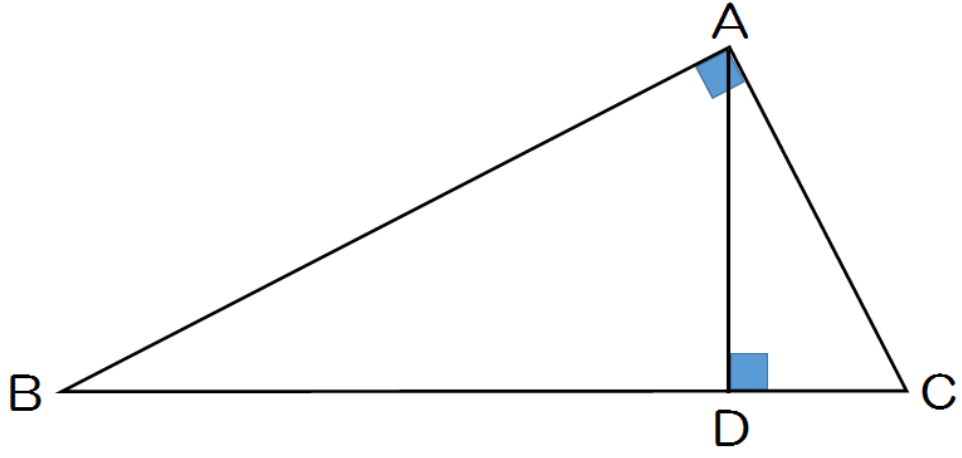



相似の証明問題でマスターしておきたい3つのパターン Qikeru 学びを楽しくわかりやすく



相似条件と証明 中学3年 数学クラブ



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス
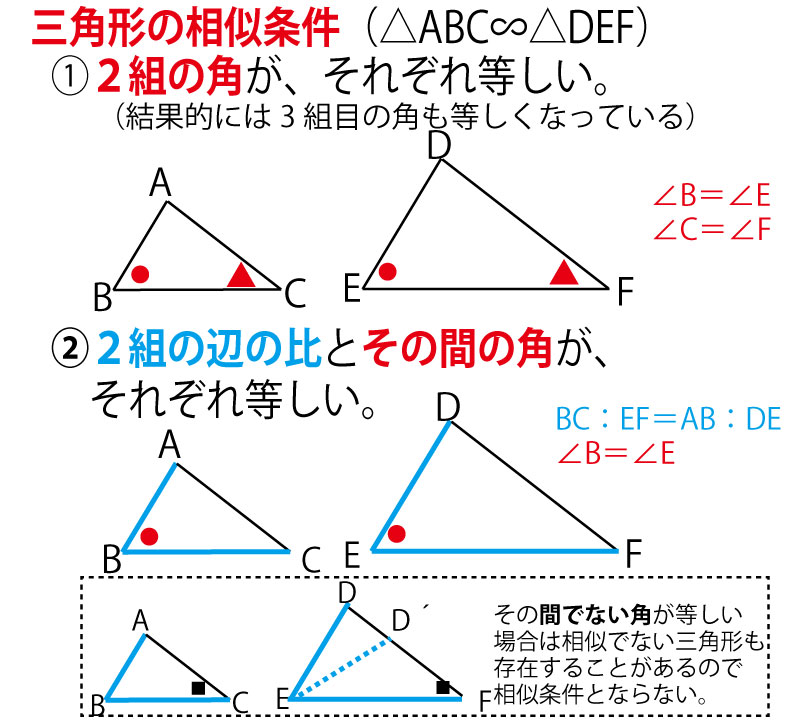



19年前期 千葉県公立高校入試 数学 第4問 図形の証明 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中学数学 理科 寺子屋塾の復習サイト 三角形と合同の証明 総合




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく




三角形の相似条件
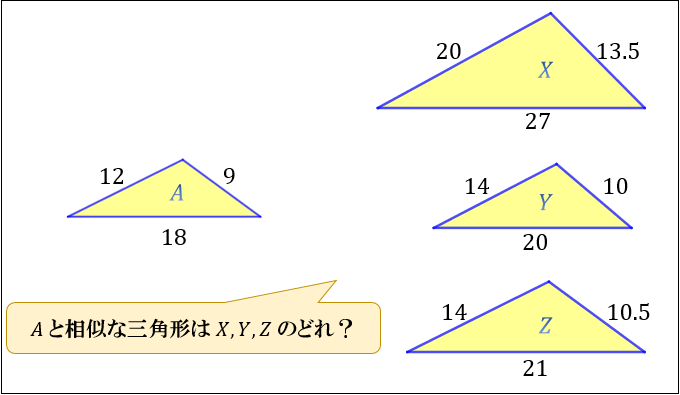



三角形の相似条件について 図解で分かる相似条件 アタリマエ




中3数学 相似の証明問題 練習編 映像授業のtry It トライイット




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく




5章1節2 三角形の相似条件2 数学のすすめ




無料 中3数学 標準問題 解答プリント 327 図形の相似2 相似条件と証明
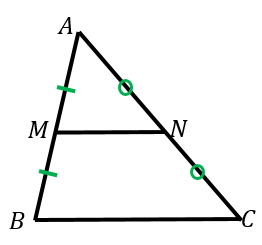



三角形の相似条件と有名な例題3問 具体例で学ぶ数学



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス
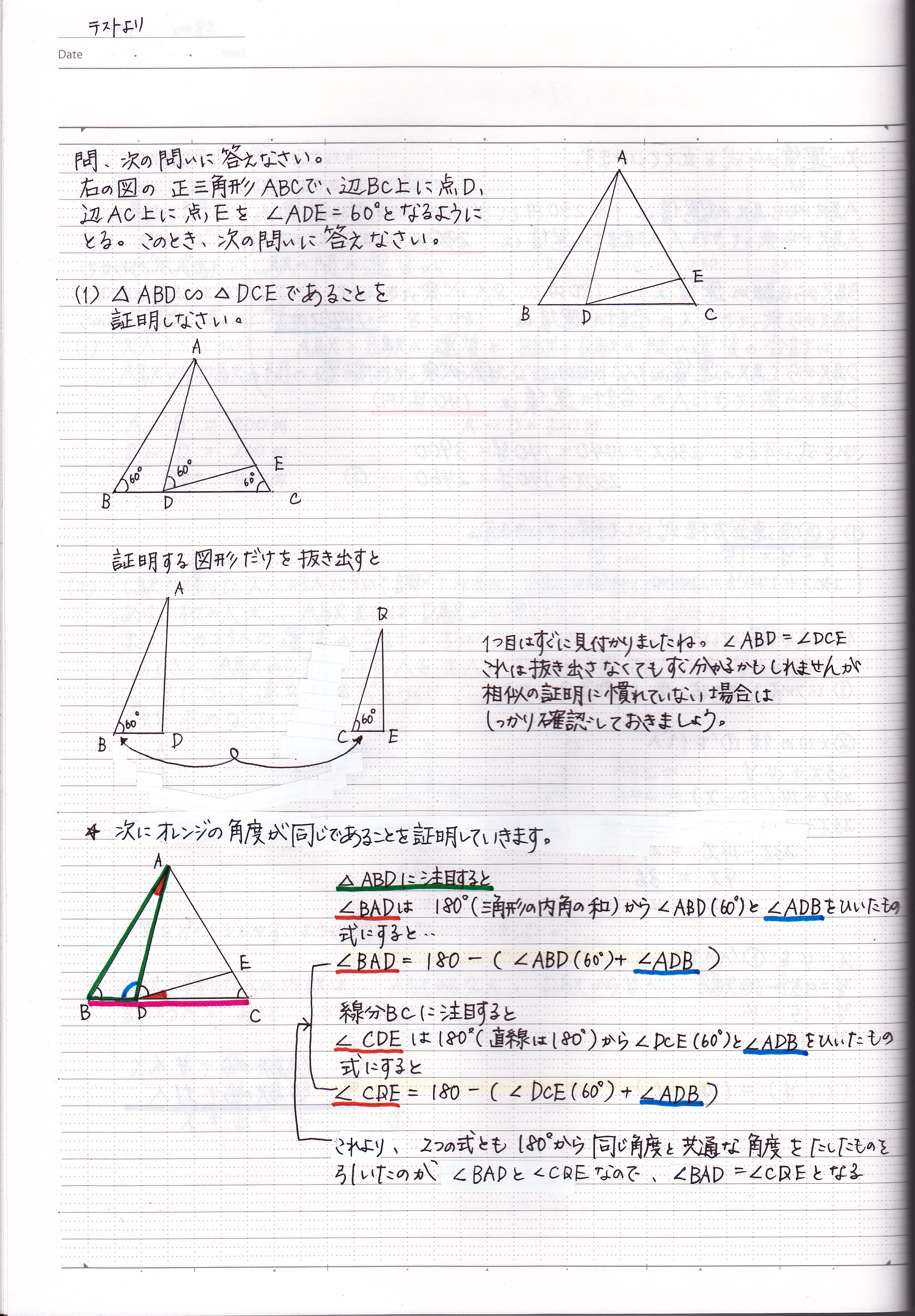



三角形の相似の証明の解き方 現役塾講師のわかりやすい中学数学の解き方
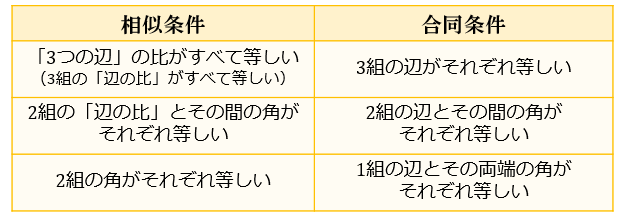



三角形の合同条件 相似条件と合同条件の違いとは アタリマエ




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学




中学数学 図形の相似




三角形の相似の証明の解き方 2 現役塾講師のわかりやすい中学数学の解き方




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学
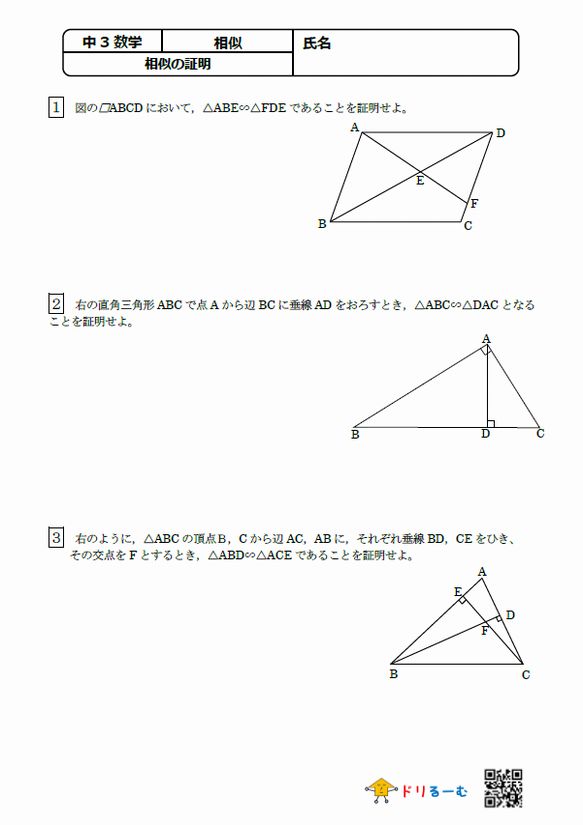



三角形の相似条件 ドリるーむ




三角形の相似条件と証明問題の解き方 数学fun
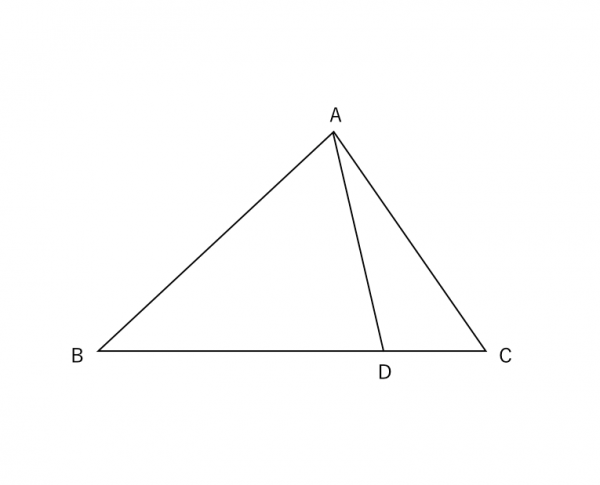



相似条件を上手く利用するポイント 苦手な数学を簡単に



相似条件と証明 中学3年 数学クラブ




数学 中3 48 相似の証明チャレンジ Lv 3 Youtube



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス




証明 合同 相似 が苦手な人へ 教遊者




中3数学 三角形の相似条件1 3辺の比 練習編 映像授業のtry It トライイット
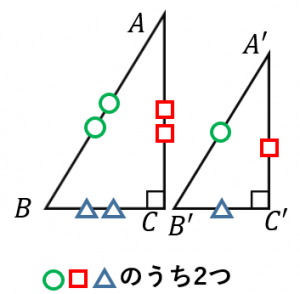



直角三角形の相似条件 具体例で学ぶ数学



Studydoctor正三角形と相似の証明 中3数学 Studydoctor




相似の証明 チーム エン




三角形の相似条件
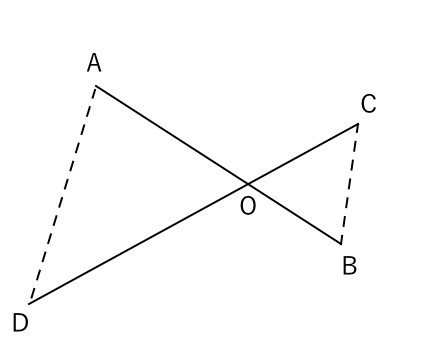



相似な図形 証明に慣れよう 苦手な数学を簡単に




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく




無料 中3数学 基本問題 解答プリント 図形の相似2 相似条件と証明



第5章6 三角形の相似 三角形の相似条件と証明 中学生




証明 合同 相似 が苦手な人へ 教遊者



14年前期 千葉県公立高校入試 数学 第4問 図形の証明 配点15点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ




3 11c A Descubre Como Resolverlo En Qanda



2分でわかる 三角形の3つの相似条件 Qikeru 学びを楽しくわかりやすく
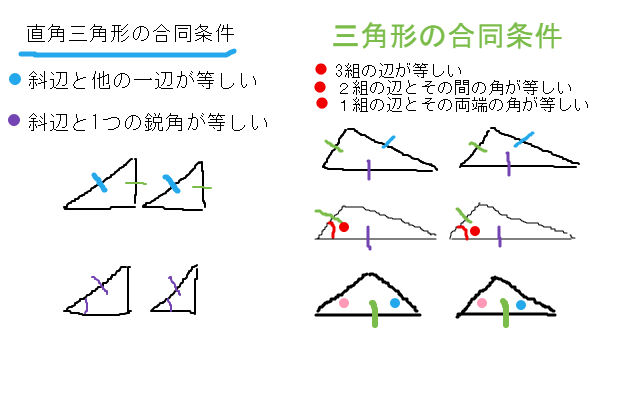



三角形 合同 相似条件 直角三角形の合同条件 中学数学 理科 寺子屋塾の復習サイト
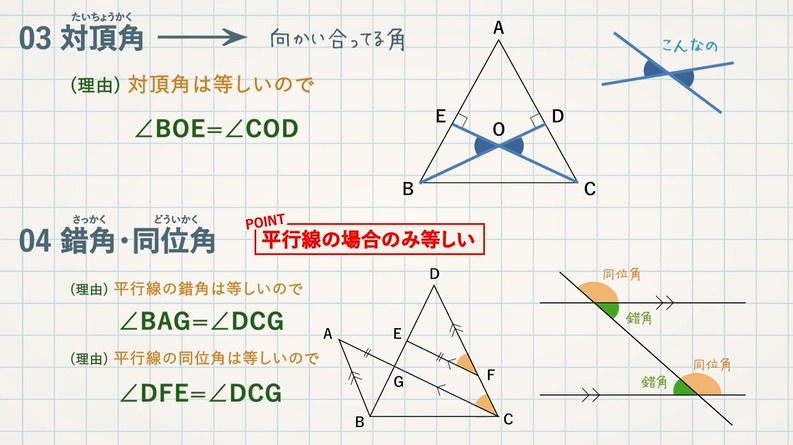



証明 合同 相似 が苦手な人へ 教遊者



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス




三角形の相似条件が見やすい図で一発理解できる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




直角三角形の合同条件 証明のときに直角三角形が出てきたらこれ 中学や高校の数学の計算問題




5章1節2 三角形の相似条件2 数学のすすめ




3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ



1




三角形の合同条件 証明のときに絶対にしておかないといけない問題 中学や高校の数学の計算問題



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス



中学校数学 証明のコツ 相似



0 件のコメント:
コメントを投稿